12.22
冬至/考研
一年中黑夜最漫长的一天
愿考神与你同在

建筑学考研最大的优势是不用考数学。
这让那些初二弯腰捡了支笔后,就再也没听懂数学课的学酥学沫学渣学灰们再次燃起了成为学霸的小火苗,想想就有点小激动~
以至于都忽略了建筑学考研要考6小时快题设计这一单虐画图狗的无人性科目。

话说回来,考快题虽然痛苦但大家自我感觉都相当不错——不管怎样你也会画满两张纸交上去吧?
可数学这个玩意儿,你除了写个“解”或“证明”,就真的无事可做了啊~

所以,建筑学就是我等数学渣们的指路明灯、敲门板砖,与数学霸们划清界限的钢筋混凝土啊~
可偏偏就有那么一群讨厌的人,数学经常满分就很令人讨厌了,但最令人无法容忍的是他们竟然来
学!建!筑!

比如下面这位看起来人畜无害的小哥。

这位“盐系”小哥名叫YuMonoeda,是个标准的80后。毕业后从2010年开始跟着隈研吾干了四年,而后在2014年成立了自己的事务所——Yu Momoeda Architecture Office(百枝优建筑事务所)。
小哥是个暖男,事务所官网的个人介绍放的是自己和亲闺女的合影。可是暖男“暖不起”事务所的生意:项目数量寥寥,勉强温饱。
直到2016年完成了一个叫做Agri礼堂(Agri Chapel)的小建筑后才开始崭露头角。这个建筑你一定也在各大网站杂志上见过——




这个仅有120余平米的小教堂坐落于日本九州岛西北海岸的国家公园内。对于观者而言,这是显而易见的森林概念;而对于设计者Yu Monoeda桑而言,这不过是一道数学题。



这设计看似很是简单,却是和大名鼎鼎的毕达哥拉斯有关系:

谈到毕达哥拉斯,数学渣们的反应可能是:

有点良心,还算对得起初中数学老师的一般人可能还记得有个叫做“毕达哥拉斯定理”东西,也就是我们常说的勾股定理(勾三股四弦五)。

而数学霸们会瞬间联想到有个叫做
“毕达哥拉斯树”的东西。
恰巧Yu Monoeda桑就是个学霸。
划重点:
毕达哥拉斯树,也叫"勾股树"。是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形。
典型的形式就是下面这个样子(图中所有出现的矩形均为正方形,三角形均为等腰直角三角形):

拓展下,我们还可以把上面的等腰直角三角形换成其他特殊形式的三角形
例如:
一般的等腰三角形:

正三角形:


当然,这种类似“从前有座山,山里有个庙”的形式可以无限延续下去,而这一类的图形也可以归类为“分形几何”(Fractal Geometry)。
分形几何学是一门以不规则几何形态为研究对象的几何学。相对于传统几何学的研究对象为整数维数,如,零维的点、一维的线、二维的面、三维的立体乃至四维的时空。分形几何学的研究对象为分数维数,如0.63、1.58、2.72。因为它的研究对象普遍存在于自然界中,因此分形几何学又被称为"大自然的几何学"。简单的说,分形就是研究无限复杂具备自相似结构的几何学。
但是,这种平面图形似乎和三维形态的建筑并不能扯上关系。毕达哥拉斯再牛b,“他的树”长了五十轮撑死也就是一棵价值五块五的“西兰花”。

经过五十步构造后的毕达哥拉斯树

罗马西兰花(花椰菜)显微放大图
所以说,不怕学渣做方案,就怕学霸搞建筑。
学霸Yu Monoeda把它进行了改进——拓展到了三维。
平面的毕达哥拉斯树包含正方形和某一种特殊三角形,两者通过一条边相连。
那么,“三维的毕达哥拉斯树”应该是由包含正方形和某一种特殊三角形的两个“几何体”组成,两者通过一个面相连。
最终这两个几何体被确定为正方体和侧面为正三角形的四棱锥。
Yes,
you have a 正方体,
you have a 四棱锥.

先别懵逼,我们再来理理基本关系。
从“单支”开始:
a.取正方体汇聚于某一顶点上的三条棱的中点并两两相连,然后用这三条连线所构成的面切去正方体的一角并得到切割截面A

b.以切割截面A为一个面作侧面为正三角形的四棱锥

c.以四棱锥底面为一个面作正方体

不断重复上述操作,经过若干“分形”后,可以得到如下的形式

回到建筑本身,“四支”同时开始:
首先依照上述的原则在原始正方体上进行多轮操作最终得到一个标准形:完整的三维分形结构。

然后仅提取出斜向和竖向的线得到整体杆件结构,并根据建筑形体的控制删除多余的杆件。

再然后根据建筑高度需求压低整体高度

最后将竖向杆拉长至斜向杆统一水平高度,采用钢索拉结各部并在每根竖向杆上另增四根斜杆。

目前为止,内部框架的宏观建构逻辑全部完成。
此时,整个构架可以看做是由三层树状单元叠合形成。从顶视图上看,三层的构成单元在尺寸上恰好形成 √2的倍数关系。
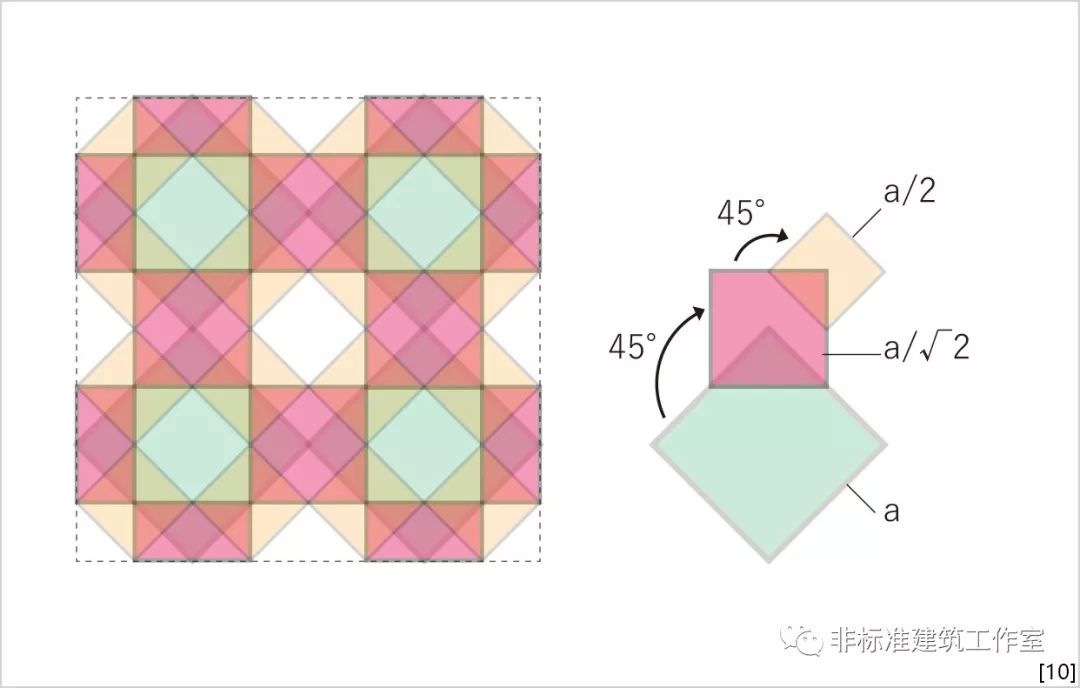
而在局部的处理上,为了更好地传达受力关系,竖向杆被划分成由五根杆件组成的“集束柱”。八根斜向杆均匀的布置在周围,并通过卡件和柱身相固定.

同时,为了减轻整体构架的重量,经过结构计算,在满足强度的要求下,三层杆件的尺寸分别定为60*60mm、90*90mm与120*120mm,大致也呈现出1:√2:2的倍数关系。

最后的最后,在这一木构架角部增设片墙,加设顶盖,数学学霸的满分作业就此完成。


这个案例好像再次证明了“数学是一切科学之母”。
但一切神化的东西对我们都没意义。
要我说,这只能说明在建筑这一行中,你身上的任何闪光点都能镶嵌成设计的钻石。
还有10天。
坚持,挺住。

本文感谢大师姐林雅楠的文字编辑和指导
本文图片
图[1]、[2]、[3]、[11]、来自https://www.architectmagazine.com
图[6]、[12]、[13]来自https://divisare.com
图[4]、[7]、[10]、[14]来自http://www.archdaily.cn
图[5]来自https://www.yumomoeda.com/
图[8] 、[9]来自《混沌与分形——科学的新疆界》
其余分析图与动图全为作者自绘,转载请注明



 下载手机APP
下载手机APP
 关注微信公众号
关注微信公众号

















































